|
|
| (64 intermediate revisions by 4 users not shown) |
| Line 1: |
Line 1: |
| [[Image:reflexion totale interne.png|thumb|right|250px|The larger the angle to the normal, the smaller is the fraction of light transmitted, until the angle when '''total internal reflection''' occurs. (The color of the rays is to help distinguish the rays, and is not meant to indicate any color dependence.)]] | | <table id="toc" style="width: 100%"> |
| '''Total internal reflection''' is an [[optical phenomenon]] that occurs when a ray of light strikes a medium boundary at an angle larger than the '''critical angle''' with respect to the normal to the surface. If the [[refractive index]] is lower on the other side of the boundary no light can pass through, so effectively all of the light is [[Reflection (physics)|reflected]]. The critical angle is the [[angle of incidence]] above which the total internal reflection occurs.
| | <tr> |
| | <td style="text-align: left; width: 33%">[[Optical Fibers|Previous Topic]]</td> |
| | <td style="text-align: center; width: 33%">[[Main_Page#Optical Fibers, Waveguides, and Lasers|Return to Optical Fibers, Waveguides, and Lasers Menu]]</td> |
| | <td style="text-align: right; width: 33%">[[Planar Dielectric Waveguides|Next Topic]]</td> |
| | </tr> |
| | </table> |
|
| |
|
| When [[light]] crosses a boundary between materials with different [[refractive index|refractive indices]], the light beam will be partially [[refraction|refracted]] at the boundary surface, and partially reflected. However, if the [[angle of incidence]] is greater (i.e. the ray is closer to being parallel to the boundary) than the critical angle — the angle of incidence at which light is refracted such that it travels along the boundary — then the light will stop crossing the boundary altogether and instead be totally reflected back internally. This can only occur where light travels from a medium with a higher [[refractive index]] to one with a lower refractive index. For example, it will occur when passing from [[glass]] to [[Earth's atmosphere|air]], but not when passing from air to glass.
| | == Total Internal Reflection == |
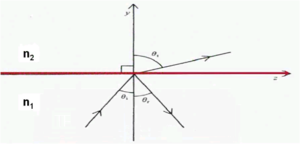
| | [[Image:Snellslaw.png|thumb|300px| When θ<sub>1</sub> > θ<sub>1c</sub> light can not enter medium n<sub>2</sub>]] |
|
| |
|
| ==Optical description==
| | A critical concept in the case of optical fibers is the concept of total internal reflection. The bending of light as it goes from one medium into another is related to the index of reflection of the materials (n<sub>1</sub> and n<sub>2</sub>). By Snell's law when n<sub>1</sub> > n<sub>2</sub> then θ <sub>1</sub> is less than θ<sub>2</sub>. As you decrease the angle θ<sub>1</sub> and bring the light closer to parallel with the interface you reach a critical angle θ<sub>1c</sub> where there is total internal reflection. |
| [[Image:Total internal reflection.jpg|thumb|250px|Total internal reflection]]
| |
| [[Image:TIR in PMMA.jpg|thumb|250px|Total internal reflection in a block of [[PMMA]]]]
| |
| Total internal reflections can be demonstrated using a semi-circular glass block. A "ray box" shines a narrow beam of light (a "[[Ray (optics)|ray]]") onto the glass. The semi-circular shape ensures that a ray pointing towards the centre of the flat face will hit the curved surface at a right angle; this will prevent refraction at the air/glass boundary of the curved surface.
| |
| At the glass/air boundary of the flat surface, what happens will depend on the angle.
| |
| Where θ<sub>c</sub> is the critical angle (measured normal to the surface):
| |
| *If θ < θ<sub>c</sub>, as with the red ray in the above figure, the ray will split. Some of the ray will reflect off the boundary, and some will refract as it passes through.
| |
| *If θ > θ<sub>c</sub>, as with the blue ray, the entire ray reflects from the boundary. None passes through. This is called total internal reflection.
| |
|
| |
|
| This physical property makes [[optical fiber]]s useful, and [[rainbow]]s and prismatic [[binoculars]] possible. It is also what gives [[diamond]]s their distinctive sparkle, as diamond has an extremely high refractive index.
| | Snells laws are also known as Fresnel's Equations: |
|
| |
|
| ==The Critical angle==
| | :<math>\theta _i = \theta _r\,\!</math> |
| ''The critical angle'' is the angle of incidence ''above'' which total internal reflection occurs. The angle of incidence is measured with respect to the [[Surface normal|normal]] at the refractive boundary. The critical angle <math>\theta_c</math> is given by:
| |
|
| |
|
| :<math>\theta_c = \arcsin \left( \frac{n_2}{n_1} \right), </math>
| | and |
|
| |
|
| where <math>n_2</math> is the [[refractive index]] of the less dense [[Medium (optics)|medium]], and <math>n_1</math> is the refractive index of the denser medium.
| | :<math>\frac {sin \theta_i} {\theta_t} = \frac {n_2} {n_1}\,\!</math> |
|
| |
|
| If the incident ray is precisely at the critical angle, the refracted ray is [[tangent]] to the boundary at the point of incidence. If for example, visible light were traveling from a glass (i.e. Lucite with an index of refraction of 1.50) into air (with an index of refraction of 1.00). The calculation would give the critical angle for light from Lucite into air, which is
| | where |
| :<math>\theta _{c}=\arcsin \left( 1.00/1.50 \right)=41.8{}^\circ </math>. | | :<math>\theta_i\,\!</math> is the angle of incidence |
| Light incident on the border with an angle less than 41.8° would be partially transmitted, while light incident on the border at larger angles with respect to normal would be totally internally reflected.
| |
|
| |
|
| The critical angle for [[diamond]] in air is about 24.4°, which means that light is much more likely to be internally reflected within a diamond. Diamonds for jewelry are [[Diamond cut|cut]] to take advantage of this; in particular the [[brilliant cut]] is designed to achieve high total reflection of light entering the diamond, and high [[dispersion (optics)|dispersion]] of the reflected light (known to jewelers as ''fire'').
| | :<math>\theta_r\,\!</math> is the angle of reflection |
|
| |
|
| If the fraction: <math>\frac{n_2}{n_1}</math> is greater than 1, then arcsine is not defined--meaning that total internal reflection does not occur even at very shallow or grazing incident angles.
| | :<math>\theta_{c} = sin^{-1}(\frac {n_2} {n_1} )\,\!</math> |
|
| |
|
| So the critical angle is only defined for <math>\frac{n_2}{n_1}\leq1</math>.
| | where: |
| | :<math>\theta_{c}\,\!</math> is the critical angle |
|
| |
|
| ==Evanescent wave==
| | :<math>n_1 , n_2\,\!</math> are the index of refraction of the two media |
| An important side effect of total internal reflection is the propagation of an [[evanescent wave]] across the boundary surface. Essentially, even though the entire incident wave is reflected back into the originating medium, there is some penetration into the second medium at the boundary. This wave can lead to a phenomenon known as frustrated total internal reflection. Additionally, the evanescent wave appears to travel along the boundary between the two materials, leading to the [[Goos-Hänchen shift]].
| |
|
| |
|
| == Frustrated total internal reflection ==
| |
| Under "ordinary conditions" it is true that the creation of an [[evanescent wave]] does not affect the conservation of energy, i.e. the evanescent wave transmits zero net energy. However, if a third medium with a higher [[refractive index]] than the second medium is placed within less than several wavelengths distance from the interface between the first medium and the second medium, the evanescent wave will be different from the one under "ordinary conditions" and it will pass energy across the second into the third medium. (See [[evanescent wave coupling]].)
| |
|
| |
|
| A transparent, low refractive index material is sandwiched between two prisms of another material. This allows the beam to "tunnel" through from one prism to the next in a process very similar to [[quantum tunneling]] while at the same time altering the direction of the incoming ray.
| | if θ<sub>1</sub> keeps Increasing: θ<sub>2</sub> approaches 90° |
|
| |
|
| ==Applications==
| | for a critical angle Θ<sub>1</sub>, Θ<sub>2</sub> = 90°and the beam emerges along the surface |
| * [[Optical fiber]]s, which are used in [[endoscope]]s and [[telecommunications]].
| |
| * [[Rain sensor#Automotive Sensors|Rain sensors]] to control automatic [[Windscreen wiper#History|windscreen/windshield wiper]]s.
| |
| * Another interesting application of total internal reflection is the spatial filtering of light.<ref>{{cite journal |url=http://planck.reduaz.mx/~imoreno/Publicaciones/OptLett2005.pdf |format=PDF |title=Thin-film spatial filters |first=Ivan |last=Moreno |authorlink=Ivan Moreno |coauthors=J. Jesus Araiza, Maximino Avendano-Alejo |journal=Optics Letters |volume=30 |number=8 |pages=pp. 914–916 |doi=10.1364/OL.30.000914 |year=2005}}</ref>
| |
| * [[Multi-touch]] screens [http://www.multitouch.nl/] use frustrated total internal reflection in combination with a camera and appropriate software to pick up multiple targets.
| |
| * [[Gonioscopy]] to view the anatomical angle formed between the eye's [[cornea]] and [[Iris (anatomy)|iris]].
| |
| * [[Gait analysis]] instrument, CatWalk [http://www.noldus.com/catwalk], use frustrated total internal reflection in combination with a high speed camera to capture and analyze footprints of laboratory rodents.
| |
|
| |
|
| ==Examples in everyday life==
| | When |
| [[Image:Total internal reflection of Chelonia mydas .jpg|Total internal reflection of the turtle can be seen at the air-water boundary.|thumb]]
| |
| Total internal reflection can be observed while swimming, if one opens one's eyes just under the water's surface. If the water is calm, its surface appears mirror-like.
| |
|
| |
|
| One can demonstrate total internal reflection by filling a sink or bath with water, taking a glass tumbler, and placing it upside-down over the plug hole (with the tumbler completely filled with water). While water remains both in the upturned tumbler and in the sink surrounding it, the plug hole and plug are visible since the angle of refraction between glass and water is not greater than the critical angle. If the drain is opened and the tumbler is kept in position over the hole, the water in the tumbler drains out leaving the glass filled with air, and this then acts as the plug. Viewing this from above, the tumbler now appears mirrored because light reflects off the air/glass interface.
| | :<math>\theta_2 = 90° \rightarrow sin \theta_2 = 1\,\!</math> |
|
| |
|
| Another very common example of Total Internal Reflection is a critically cut [[diamond]]. This is what gives it maximum sparkle.
| | :<math>\theta_{1c} = sin^{-1} \left (\frac {n_2} {n_1} \right )\,\!</math> |
|
| |
|
| ==See also==
| |
| *[[Evanescent wave]]
| |
| *[[Perfect mirror]]
| |
| *[[Refraction]]
| |
| *[[Refractive index]]
| |
| *[[Fresnel equations]]
| |
| *[[Snell's window]]
| |
| *[[Goos-Hänchen effect]]
| |
|
| |
|
| ==References==
| | and when |
| {{reflist}}
| |
| *[[Federal Standard 1037C]] and [[MIL-STD-188]]
| |
|
| |
|
| ==External links==
| | :<math>\theta_1 > \theta_{1c}\,\!</math> there is total reflection |
| * [http://cs.nyu.edu/~jhan/ftirsense/index.html FTIR Touch Sensing]
| |
| * [http://cs.nyu.edu/~jhan/ftirtouch/index.html Multi-Touch Interaction Research]
| |
| * [http://www.i-bar.ch/index.php?id=88&L=1 iBar Intelligent Surface System]
| |
| * http://hyperphysics.phy-astr.gsu.edu/hbase/phyopt/totint.html
| |
| * [http://demonstrations.wolfram.com/TotalInternalReflection/ Total Internal Reflection] by Michael Schreiber, [[Wolfram Demonstrations Project]]
| |
| * [http://www.noldus.com/catwalk CatWalk] by [http://www.noldus.com/ Noldus Information Technology]
| |
|
| |
|
| {{Commons|Total internal reflection}}
| | In this case there is no transmitted light in the second medium (the irradiance of the reflected and incident beams is equal). Light interacts at the interface and there is a phase shift between the incident and the reflected beams which is dependent on the two materials. |
| | |
| | This is a critical process in optical fibers and waveguides because it can carry light for long distances. For these values of index of refraction you get a critical angle of 78.6 which means the light must be very nearly parallel to the interface. |
| | |
| | for n<sub>1</sub> = 1.53 and n<sub>2</sub> = 1.50 : θ<sub>1c</sub> = 78.6° |
| | |
| | |
| | |
| | <br clear='all'> |
| | |
| | === Simulations === |
| | |
| | |
| | This flash simulation shows how total internal reflection and minimum radius of turns depends on the diameter of the optical fiber. The diameter changes how much of the light is below the critical angle where it is fully reflected. |
| | |
| | <swf width="500" height="400">http://concave.stc.arizona.edu/thepoint/Interactive/ofiber.swf</swf> |
| | |
| | |
| | This simulation allows you to select combinations of materials with different indexes of refraction. Try to get the best combination to achieve total internal reflection. |
| | <swf width="500" height="400">http://concave.stc.arizona.edu/thepoint/Interactive/ofiberapp2.swf</swf> |
| | |
| | [[category:light]] |
| | <table id="toc" style="width: 100%"> |
| | <tr> |
| | <td style="text-align: left; width: 33%">[[Optical Fibers|Previous Topic]]</td> |
| | <td style="text-align: center; width: 33%">[[Main_Page#Optical Fibers, Waveguides, and Lasers|Return to Optical Fibers, Waveguides, and Lasers Menu]]</td> |
| | <td style="text-align: right; width: 33%">[[Planar Dielectric Waveguides|Next Topic]]</td> |
| | </tr> |
| | </table> |
Total Internal Reflection
When θ
1 > θ
1c light can not enter medium n
2A critical concept in the case of optical fibers is the concept of total internal reflection. The bending of light as it goes from one medium into another is related to the index of reflection of the materials (n1 and n2). By Snell's law when n1 > n2 then θ 1 is less than θ2. As you decrease the angle θ1 and bring the light closer to parallel with the interface you reach a critical angle θ1c where there is total internal reflection.
Snells laws are also known as Fresnel's Equations:
- <math>\theta _i = \theta _r\,\!</math>
and
- <math>\frac {sin \theta_i} {\theta_t} = \frac {n_2} {n_1}\,\!</math>
where
- <math>\theta_i\,\!</math> is the angle of incidence
- <math>\theta_r\,\!</math> is the angle of reflection
- <math>\theta_{c} = sin^{-1}(\frac {n_2} {n_1} )\,\!</math>
where:
- <math>\theta_{c}\,\!</math> is the critical angle
- <math>n_1 , n_2\,\!</math> are the index of refraction of the two media
if θ1 keeps Increasing: θ2 approaches 90°
for a critical angle Θ1, Θ2 = 90°and the beam emerges along the surface
When
- <math>\theta_2 = 90° \rightarrow sin \theta_2 = 1\,\!</math>
- <math>\theta_{1c} = sin^{-1} \left (\frac {n_2} {n_1} \right )\,\!</math>
and when
- <math>\theta_1 > \theta_{1c}\,\!</math> there is total reflection
In this case there is no transmitted light in the second medium (the irradiance of the reflected and incident beams is equal). Light interacts at the interface and there is a phase shift between the incident and the reflected beams which is dependent on the two materials.
This is a critical process in optical fibers and waveguides because it can carry light for long distances. For these values of index of refraction you get a critical angle of 78.6 which means the light must be very nearly parallel to the interface.
for n1 = 1.53 and n2 = 1.50 : θ1c = 78.6°
Simulations
This flash simulation shows how total internal reflection and minimum radius of turns depends on the diameter of the optical fiber. The diameter changes how much of the light is below the critical angle where it is fully reflected.
<swf width="500" height="400">http://concave.stc.arizona.edu/thepoint/Interactive/ofiber.swf</swf>
This simulation allows you to select combinations of materials with different indexes of refraction. Try to get the best combination to achieve total internal reflection.
<swf width="500" height="400">http://concave.stc.arizona.edu/thepoint/Interactive/ofiberapp2.swf</swf>
