Difference between revisions of "Introduction to Third-order Processes and Materials"
Cmditradmin (talk | contribs) |
Cmditradmin (talk | contribs) |
||
| (108 intermediate revisions by 4 users not shown) | |||
| Line 7: | Line 7: | ||
</table> | </table> | ||
The term "third order nonlinear optical (NLO) materials" refers to materials whose polarization depends on the intensity of an applied electromagnetic field. This intensity dependence gives rise to a variety of useful properties such as self-focusing, two-photon absorption, and third harmonic generation. | |||
== Hyperpolarizability == | == Nonlinear Susceptibility and Hyperpolarizability == | ||
For a material in an electric field, the bulk polarization, ''P'', can be expanded as follows : | |||
:<math>P = P_0 + \chi^{(1)}·E + (1/2)\chi^{(2)}·· E^2 + (1/6)\chi^{(3)}···E^3+ ...\,\!</math> (1) | |||
where: | |||
= | :<math>P_0\,\!</math> is the polarization in the absence of a field (some materials, such as polyvinylene difluoride when poled, can have a finite bulk polarization in the absence of an applied field), | ||
:<math>\chi^{(1)}\,\!</math> is the susceptibility of the material (which is related to the dielectric constant; see [[http://depts.washington.edu/cmditr/mediawiki/index.php?title=Quantum-Mechanical_Theory_of_Molecular_Polarizabilities]]), | |||
:<math>\chi^{(2)}\,\!</math> and <math>\chi^{(3)}\,\!</math> are the second- and third-order susceptibilities, respectively, | |||
:<math>E\,\!</math> is the applied electric field, | |||
(more generic expressions can be written instead of (1), if more than one field is present). | |||
Because of symmetry, <math>\chi^{(2)}\,\!</math> is non-zero only if the material is not centrosymmetric overall (i.e., a centrosymmetry arrangement of noncentrosymmetric molecules leads to <math>\chi^{(2)}\,\!</math> = 0). Similarly, higher order <math>\chi^{(n)}\,\!</math> with even ''n'' are zero in centrosymmetric materials. There are no symmetry restrictions, instead, on <math>\chi^{(n)}\,\!</math> when ''n'' is odd (that is, these susceptibilities can be finite in centrosymmetric materials). | |||
''P'' and ''E'' are vectors and the linear susceptibility <math>\chi^{(1)}\,\!</math> is a 3 x 3 tensor; the susceptibilities <math>\chi^{(n)}\,\!</math> are higher-rank tensors (3 x 3 x 3 for n = 2, 3 x 3 x 3 x 3 for n = 3, etc.). The specific component of the relevant tensor is usually represented by subscripted indices (e.g., <math>\chi_{ijk}^{(2)}\,\!</math>, where ''i'', ''j'', ''k'' are one of the cartesian coordinates). The linear and nonlinear susceptibilities depend on the frequency/frequencies (wavelength/wavelengths) of the electromagnetic field and are material's properties. | |||
Nonlinear contributions to the material's polarization become more important with increasing field strength, since they scale with higher powers of the field. | |||
=== Taylor Expansion for Molecular Dipole Moment === | |||
In a manner similar to (1), at the molecular level, the dipole moment of a molecule, ''μ'', is affected by an external electric field and it can be expanded in a Taylor series as a function of the field: | |||
:<math>\mu = \mu_0 + \alpha E + (1/2)\beta ·· E^2 + (1/6)\gamma ···E^3+ ...\,\!</math> (2) | |||
where: | |||
:<math>\mu_0\,\!</math> is the permanent dipole of the molecule, | |||
:<math>\alpha\,\!</math> is the polarizability of the molecule (the microscopic equivalent to <math>\chi^{(1)}\,\!</math>), | |||
:<math>\beta\,\!</math> and <math>\gamma\,\!</math> are the first and second hyperpolarizabilities, respectively. | |||
As for the susceptibilities, <math>\alpha\,\!</math>, <math>\beta\,\!</math>, and <math>\gamma\,\!</math> are tensors of progressively higher rank, are frequency dependent, and each component can be a complex quantity. | |||
<math>\beta\,\!</math> is zero for centrosymmetric molecules. | |||
Under normal conditions, | |||
:<math>\alpha_{ij} E_j > \beta_{ijk} E_j · E_k > \gamma_{ijkl} E_j · E_k · E_l \,\!</math> | |||
(here we have introduced the subscript to identify a specific component of the tensors and vectors; ''i'', ''j'', ''k'', ''l'' = ''x'', ''y'', ''z''). | |||
However, for field strengths large enough or for specific frequencies of the electromagnetic field, one of the nonlinear terms may become the dominant contribution to the dipole moment. | |||
Typically, high intensity laser beams are need for the effects of the hyperpolarizabilities to become observable. | |||
=== Third-order Nonlinear Polarization of Matter === | |||
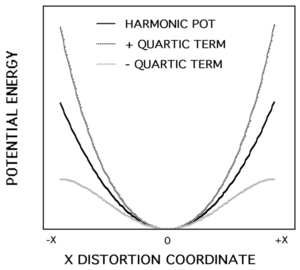
[[Image:Harmonic_quartic.png|thumb|300px|Deviation from simple harmonic potential with a positive or negative quartic term.]] | |||
It can be shown that the description of Eq. (2) above corresponds to the behavior of a molecule in an anharmonic potential well. Second-order NLO effects arise from a cubic component in the potential as a function of displacement from the equilibrium position. A quartic term in the potential is at the origin of third-order effects. This is illustrated in the graph at right. If the correction is added in a positive way the well becomes steeper, adding the correction in a negative way the potential well is more shallow. The change is symmetric with respect to x = 0. The curves shown are greatly exaggerated, in reality the deviation would be less than the thickness of the lines as they are drawn. For the most part during normal oscillations the electrons are held within a quadratic potential. Only when there is a large electric field is there a deviation of the electron from their resting position to the point where these terms (terms which account for anharmonicity) are manifested in any significant way. When a restoring force of x<sup>4</sup> is added to a molecule the polarization deviates from that characteristic of the harmonic potential. A greater displacement means that it is getting harder to polarize the molecule the greater the difference between the harmonic potential and the quartic potential. A material with a greater susceptibility has a higher refractive index (and a higher dielectric constant). If, as you polarize this material more and more it becomes harder to polarize, its susceptibility decreases with the field, as does its refractive index. | |||
<br clear='all'> | |||
== Third-Order NLO Effects == | |||
=== Nonlinear Self-Focusing === | |||
Let's consider a beam of light propagating into a NLO material with a positive nonlinear refractive index. If the intensity distribution in the beam is higher in the center than at the edge, the material that is near the center of the beam, where the intensity is highest, will have a higher refractive index than the material at the edge of the beam profile, where there is low intensity. The refractive index changes because in this NLO material the polarizability (and susceptibility) depends in the intensity of the light, and thus the refractive index is also intensity dependent. As the refractive index is now different across the beam profile, the different portions of the beam will be refractive to different degrees, in particular the rays near the optical axis are refractive more than rays farther away from the axis. Thus this NLO material behaves like a lens that focuses light that propagates through it. In a focusing beam the cross-sectional area of the beam decreases as you approach the focal point and the intensity increases (because there are more photons in the unit area). So, as a beam becomes focused the added intensity increases the refractive index further, causing even more focussing, higher intensity at the center of the beam and more change in refractive index. This process is called “'''nonlinear self-focusing'''”. | |||
[[Image:Grin-lens.png|thumb|300px|A gradient-index lens with a parabolic variation of refractive index (n) with radial distance (x). The lens focuses light in the same way as a conventional lens. A non-linear material acts like a graded index because the index changes with the intensity of the light, which is largest at the center of the beam, thus leading to focusing, even higher intensity and so on.]] | |||
All materials (including glass and air) have third order non-linear optical effects. Sometimes these effects can lead to catastrophic self-focusing, leading to the destruction of the material when the intensity becomes too high. Catastrophic self-focusing thus poses limits to the maximum intensities within optical materials, for example those used in lasers. Usually, a material with fewer defects is less likely to be damaged (or will damage at higher intensities). When doing experiments involving frequency tripling researchers need to use perfect defect-free crystals. | |||
In an NLO material in which polarization decreases with the light intensity (a material with a negative nonlinear refractive index), the opposite effect is observed: the refractive index encountered by the beam while propagating in the medium is smaller at the center of the beam and larger near the edges, leading to '''self-defocusing''' of the beam. Thus, the beam passing through this material has a tendency to spread out. | |||
Positive and negative ''γ'' and positive and negative ''χ''<sup>(3)</sup> lead to different effects. Specifically, negative ''χ''<sup>(3)</sup> leads to self-defocusing, and positive ''χ''<sup>(3)</sup> leads to self-focusing. | |||
See Wikipedia [http://en.wikipedia.org/wiki/Self-focusing Self Focusing] | |||
See also Encyclopedia of Laser Physics [http://www.rp-photonics.com/self_focusing.html Self Focusing] | |||
=== Third Harmonic Generation and the Optical Kerr Effect === | |||
If we reconsider equation (2) for the expansion of dipole moment of a molecule as a function of electric field, assuming that the even-order terms are zero (i.e., that the molecule is centrosymmetric), and we apply an oscillating field at frequency ''ω'': | |||
:<math>E = E_0 cos(\omega t) \,\!</math> | |||
the dipole moment of the molecule becomes: | |||
:<math>\mu = \alpha E_0 cos(\omega t) + (1/6) \gamma E_0^3cos^3 (\omega t) + ...\,\!</math> (3) | |||
From trigonometry it can be shown that: | |||
= | :<math>cos^3(\omega t) = (3/4) cos(\omega t) + (1/4) cos (3\omega t)\,\!</math> (4) | ||
Substituting (4) in (3), we obtain: | |||
:<math>\mu = \alpha E_0 cos(\omega t) + (1/6) \gamma E_0^3 (3/4) cos(\omega t) + (1/6) \gamma E_0^3 (1/4) cos (3\omega t)\,\!</math> | |||
or, equivalently: | |||
:<math>\mu= [\alpha +(1/6) \gamma E_{0}^{2}(3/4)]E_0cos(\omega t) + (1/6) \gamma E_0^3(1/4)cos(3\omega t)\,\!</math> (5) | |||
Thus, the material has an effective polarizability that depends on ''E''<sub>0</sub><sup>2</sup> (the maximum deviation of the sinusoidal electric field) and ''γ''. This is called Kerr effect. | |||
''E''<sub>0</sub><sup>2</sup> is always positive. On the other hand ''γ'' can be either positive or negative. Thus, by increasing the magnitude of the electric field, the polarizability of the material increases if ''γ'' is positive and decreases if ''γ'' is negative. If ''E'' is the electric field of an electromagnetic wave, due to this third-order effect the linear polarizability can be changed simply by modifying the intensity of the applied light (because the light intensity is proportional to ''E''<sub>0</sub><sup>2</sup>). | |||
This component of the dipole moment or polarization oscillates at the same frequency of the input field, ''ω''. We note that the :<math>[\alpha + (1/6) \gamma E_{0}^{2}(3/4)]\,\!</math> term of equation (5) is similar to the term leading to the linear electrooptic effect or the Pockels effect. | |||
There are two kinds of Kerr effects. | |||
In an optical frequency Kerr effect a very high intensity beam is used to changed the refractive index of a material at the same frequency the beam. | |||
The DC Kerr effect or the quadratic electro-optic effect involves a low intensity beam combined with an oscillating applied voltage that can modulate the refractive index. | |||
It can be seen that equation (5) also contain a term at frequency 3''ω'', the third harmonic of the incident field: | |||
:<math> (1/6) \gamma E_0^3(1/4)cos(3\omega t)\,\!</math> | |||
The magnitude of this component depends on ''γ''. | |||
Thus, the interaction of light with a third-order NLO material will create a polarization component at its third harmonic. | |||
Likewise, at the macroscopic level, in the presence of a strong laser beam at frequency ''ω'' the bulk material will have an induced polarization at 3''ω'', due to ''χ''<sup>(3)</sup>. This process is called third-harmonic generation. | |||
== Four Wave Mixing == | |||
Third harmonic generation is a four wave mixing process: three waves (electric fields 1, 2 and 3 at frequency ''ω'') interact in a material to create a fourth wave (at frequency 3''ω''). In the case of third harmonic generation with a single beam of light the three fields are degenerate: electric field 1 has the same frequency, phase and momentum ('''k''' vector) as electric field 2 and 3. | |||
This does not have to be the case. There could be three beams with different phases and different directions, or different polarizations. If the frequency components of the fields are different other nonlinear effects can be observed, for example, the fields can "mix" and produce new fields with frequency equal to the sums and differences of frequencies of the input fields (four wave mixing): | |||
:<math>\omega_1 + \omega_2 + \omega_3\,\!</math> (this is third harmonic generation if ''ω''<sub>1</sub> = ''ω''<sub>2</sub> = ''ω''<sub>3</sub>) | |||
or | |||
:<math>\omega_1 + \omega_2 - \omega_3\,\!</math> | |||
If the frequencies are the same, the latter situation yields light out at the same frequency as the input and is called degenerate four wave mixing (in the case of a single beam, this leads to the self-focusing effect discussed earlier). | |||
Thus, | Another way to describe the '''degenerate four wave mixing''' (DFWM) process is to consider two beams of light (at the same frequency) interacting within a material to create an interference pattern and thus a spatially periodic variation in light intensity in the material. As we have noted before, the induced change in refractive index of a third-order nonlinear optical material is proportional to the intensity of the applied field. Thus, if two beams are interfering in a third-order NLO material, the result will be a refractive index grating, that is a periodic modulation of the refractive index in the areas of constructive and destructive interference: the areas that are brightest will have an increased refractive index (with a positive ''χ''<sup>(3)</sup>); at the darkest point the refractive index will have zero change. When a third beam is incident on this grating, the beam is diffracted from the grating, generating a fourth beam, called the phase conjugate. This process is called four wave mixing: two writing beams and a probe beam result in a fourth phase-conjugate beam. | ||
=== Phase Conjugation === | === Phase Conjugation === | ||
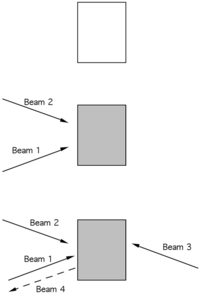
[[Image:4wavemixing.png|thumb|200px|Phase conjugate optics.]] | |||
A potential use of Degenerate Four-wave Mixing (DFWM) is in phase conjugate optics. | |||
A beam of light has a momentum determined by the direction it is traveling. If beams of light mix and do not transfer energy to the material the momentum must be conserved. Two counter-propagating beams with the same phase have a momentum sum of zero. | |||
If the probe beam is counter-propagating with respect to one of the writing beams in a DFWM configuration, then the diffracted beam exactly retraces the path of the other writing beam. | |||
Phase conjugate optics takes advantage of this special feature of the diffracted beam. | |||
As a result, a pair of diverging beams impinging on a phase conjugate mirror will converge after "reflection". | |||
In contrast, a pair of diverging beams reflected from an ordinary mirror will continue to diverge. | |||
One consequence of this is that distorted optical wavefronts can be reconstructed using phase conjugate optical systems, as described in the next subsection. | |||
<br clear='all'> | |||
=== Phase Conjugate Mirror === | |||
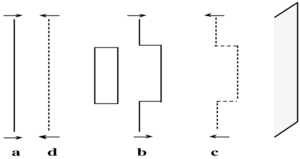
[[Image:Phaseconjugate_mirror.png|thumb|300px|Reflection from a phase conjugate mirror retraces exactly the same path and alterations as the incoming wave.]] | |||
The figure at right illustrates the operation of a phase conjugate mirror. A planar wave (a) passes through a distorting material (rectangle), which introduces an aberration in the wavefront. Then the light interacts with a phase conjugate mirror (gray area) creating the phase conjugate wavefront (c). Then the phase conjugate wave passes through the distorting material on the reverse path, canceling the original aberration thus producing an undistorted wavefront (d). | |||
Aberrations in the wavefront can be caused by the medium not having a uniform refractive index, so that portions of the light will travel faster than others, and leading to a deformation in the original wavefront. When the wavefront hits the phase conjugate mirror, the propagation direction of the beam reversed, but the shape of the wavefront is not changed: the part of the beam that comes into the mirror first ends up leaving last and viceversa. When the reversed beam travels back and encounters the original material, portions of the beam are going to be slowed, other sped up, as previously, but now the process acts on a distorted wavefront. The result is that distortion produced by the second pass exactly cancels that of the first pass, thus the aberration is removed and the original wavefront is obtained. | |||
In the following Flash animation a wavefront of light passes through a material with uneven index of refraction. Select either "normal mirror" or "phase conjugate mirror" to see the effect on the final wavefront after passing through the medium twice. | |||
<div id="Flash">Phase conjugate mirror animation</div> | |||
<swf width="500" height="400">images/e/e7/Conjugatemirror.swf</swf> | |||
There are applications for this when looking at distant objects that have passed through a material that is scattering. If you bounce the light off a phase conjugate mirror in two passes, you can get back the original undistorted image. This is useful for targeting applications and for looking at images of the Earth from a satellite where there are distortions due to inhomogeneities in the atmosphere. This is a third order nonlinear optical effect. | |||
: | See [[wikipedia:Nonlinear_optics#Optical_phase_conjugation]] | ||
== Second Hyperpolarizability and BOA == | |||
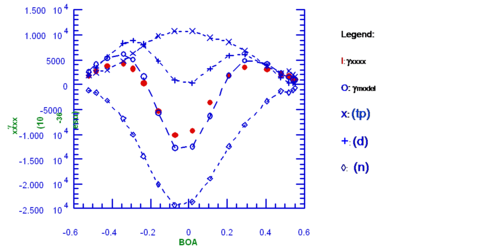
[[Image:Secondpolarizability_boa.png|thumb|500px|Contributions to ''γ'' from various terms as a function of bond-order-alternation, BOA.]] | |||
The figure at right displays how the second hyperpolarizability ''γ'' varies as a function of bond-order alternation (BOA) in a one-dimensional polymethine structure. The tensor component included in the plot is xxxx, where x represents the long axis of the molecule (the other components are negligible for these systems). As introduced elsewhere, BOA is the average value of the difference between the length of adjacent CC bonds in the chain [[http://depts.washington.edu/cmditr/mediawiki/index.php?title=Structure-Property_Relationships&action=edit§ion=3]]. | |||
The left side of the plot corresponds to the polyene limit (large and negative BOA), the cyanine-like limit corresponds to BOA = 0, and the zwitterionic limit to large and positive BOA. | |||
''γ''<sub>xxxx</sub> (red dots) is calculated using perturbation theory. It can be noted that ''γ'' starts positive in the polyene limit, goes through a maximum, then through zero before assuming a large negative value at the cyanine-like limit; the behavior is symmetrical on the BOA > 0 side of the plot . | |||
If only few states contribute to the perturbation expression for ''γ'', it is possible to write a simplified equation that contains three terms, dubbed '''n''' (negative), '''tp''' (two-photon) and '''d''' (dipolar, because it only comes into effect when there is a change in dipole moment between the ground and the excited state): | |||
:<math>\gamma_{model} \propto - \left ( \frac {\mu^{4}_{ge}} {E^{3}_{ge}} \right) + \sum_{e^\prime} \left( \frac {\mu^{2}_{ge} \mu^{2}_{ee^\prime}} {E^{2}_{ge} E_{ge^\prime}} \right ) + \left ( \frac {\mu^{2}_{ge} (\mu_{ee} - \mu_{gg})^{2}} {E^{3}_{ge}} \right )\,\!</math> | |||
where: | |||
The | ''g'' is the ground state, ''e'' the lowest excited state. The summation in the middle term is over two-photon allowed states, ''e''', in the system. | ||
:<math>\mu_{ab}\,\!</math> is the transition dipole moment between the states ''a'' and ''b''. | |||
:<math> E_{ab}\,\!</math> is the energy difference between the states ''a'' and ''b''. | |||
In the '''n''' term (leftmost term in the equation), the transition dipole moment between the ground and the initial state comes in at the 4th power and is divided by the energy gap between those two states to the third power. This term is always negative and it assumes the largest absolute value at the cyanine limit. | |||
The '''tp''' term (middle term in the equation) depends on the transition dipole moment between the ground and the excited state, and between the excited state and a higher lying two-photon state, both squared. This term is positive, with a maximum for BOA = 0. | |||
The '''d''' term (rightmost term in the equation) is similar to that that appears in simplified expressions for the hyperpolarizability ''β''. The difference in dipole moment is squared so that it always positive, the energy term is cubed. The two positive maxima in ''γ'' can be traced mostly to this term. | |||
The value of each of these terms as a function of BOA and their sum, ''γ''<sub>model</sub> (open circles), are displayed in the plot. The values of ''γ''<sub>model</sub> are similar to those of ''γ''<sub>xxxx</sub>, indicating that the simplified model is sufficient to account for the main changes in the magnitude and sign of the hyperpolarizability for this class of compounds. | |||
=== Third-order Nonlinear Optical Properties of Polarized Polyenes === | |||
[[Image:Betacarotene_NLO.png|thumb|400px|Effect on ''γ'' when various acceptors are added to beta-carotene.]] | |||
Beta-carotene is an organic compound with a long polyenic chain, it is orange-red and it is found in many fruits and vegetables. | |||
Derivatives of beta-carotene have been synthesized with acceptor groups of various strengths on one end of the chain, to test the effect on the polarizability and hyperpolarizability of the molecule. This table reports the values of ''γ'' for a series of these derivatives. It can be seen that the magnitude of ''γ'' increases by a factor of 45 when the strength of the acceptor is increased. This is also accompanied by a red-shift in the position of the absorption maximum. The increase in ''γ'' can be explained by a change in the BOA value in the presence of acceptor groups, as BOA becomes less negative going from the initial polyene (symmetric structure, no acceptor; see top row) to a molecule with strong acceptor on one side (bottom row). As seen in the plot in the previous subsection, this type of change in BOA is accompanied by an increase in ''γ''.<br clear='all'> | |||
== Summary == | |||
Third-order nonlinear effects can be described in terms of the molecular parameter hyperpolarizability ''γ'' or the bulk susceptibility ''χ''<sup>(3)</sup>. These quantities depend on the frequency of the electromagnetic waves interacting in a material and different effects can be observed as a function of these frequencies. | |||
These are also complex quantities. In the case of the linear polarizability, the real part is related to how light is refracted by the material, the imaginary part is related to the absorption of light by the material. The situation is similar for ''γ''. Molecules will have both real and imaginary parts to ''γ''. The real part affects to how the refractive index is changed as light of a given intensity goes through it (the refractive index is field-dependent in these materials). The imaginary part is manifested in two-photon absorption. An intensity dependent refractive index can lead to self-focussing or self-defocussing of a beam propagating through a layer of material. Other third-order optical effects that can be exploited for applications are sum (or difference) frequency generation and wave mixing. | |||
In order to make useful devices like the Mach Zehnder interferometer you want to use a material whose index of refraction can be changed using a light beam, but you don’t want to lose light in the material because of linear absorption or scattering. They can also lose transparency at a high intensity due to the process of two-photon absorption. The identification of materials with large ''γ''s at the desired wavelength and low loss is an active area of research. Dipolar molecules tend to have large positive ''γ'' values but also tend to have high two-photon absorption cross sections. | |||
Recently it has been reported that a class of molecules with negative ''γ'' have very large real parts of the hyperpolarizability but, in certain spectral regions , their imaginary part is almost zero so there would be no light lost due to two-photon absorption. These are good candidates for all optical switching applications because until now molecules with high ''γ'' (''χ''<sup>(3)</sup>) have had a high a loss due to two-photon absorption. | |||
see also [[All Optical Switching]] | |||
[[category:third order NLO]] | |||
<table id="toc" style="width: 100%"> | <table id="toc" style="width: 100%"> | ||
<tr> | <tr> | ||
Latest revision as of 13:47, 22 July 2010
| Return to Third-order Processes, Materials & Characterization Menu | Next Topic |
The term "third order nonlinear optical (NLO) materials" refers to materials whose polarization depends on the intensity of an applied electromagnetic field. This intensity dependence gives rise to a variety of useful properties such as self-focusing, two-photon absorption, and third harmonic generation.
Nonlinear Susceptibility and Hyperpolarizability
For a material in an electric field, the bulk polarization, P, can be expanded as follows :
- <math>P = P_0 + \chi^{(1)}·E + (1/2)\chi^{(2)}·· E^2 + (1/6)\chi^{(3)}···E^3+ ...\,\!</math> (1)
where:
- <math>P_0\,\!</math> is the polarization in the absence of a field (some materials, such as polyvinylene difluoride when poled, can have a finite bulk polarization in the absence of an applied field),
- <math>\chi^{(1)}\,\!</math> is the susceptibility of the material (which is related to the dielectric constant; see [[1]]),
- <math>\chi^{(2)}\,\!</math> and <math>\chi^{(3)}\,\!</math> are the second- and third-order susceptibilities, respectively,
- <math>E\,\!</math> is the applied electric field,
(more generic expressions can be written instead of (1), if more than one field is present).
Because of symmetry, <math>\chi^{(2)}\,\!</math> is non-zero only if the material is not centrosymmetric overall (i.e., a centrosymmetry arrangement of noncentrosymmetric molecules leads to <math>\chi^{(2)}\,\!</math> = 0). Similarly, higher order <math>\chi^{(n)}\,\!</math> with even n are zero in centrosymmetric materials. There are no symmetry restrictions, instead, on <math>\chi^{(n)}\,\!</math> when n is odd (that is, these susceptibilities can be finite in centrosymmetric materials). P and E are vectors and the linear susceptibility <math>\chi^{(1)}\,\!</math> is a 3 x 3 tensor; the susceptibilities <math>\chi^{(n)}\,\!</math> are higher-rank tensors (3 x 3 x 3 for n = 2, 3 x 3 x 3 x 3 for n = 3, etc.). The specific component of the relevant tensor is usually represented by subscripted indices (e.g., <math>\chi_{ijk}^{(2)}\,\!</math>, where i, j, k are one of the cartesian coordinates). The linear and nonlinear susceptibilities depend on the frequency/frequencies (wavelength/wavelengths) of the electromagnetic field and are material's properties. Nonlinear contributions to the material's polarization become more important with increasing field strength, since they scale with higher powers of the field.
Taylor Expansion for Molecular Dipole Moment
In a manner similar to (1), at the molecular level, the dipole moment of a molecule, μ, is affected by an external electric field and it can be expanded in a Taylor series as a function of the field:
- <math>\mu = \mu_0 + \alpha E + (1/2)\beta ·· E^2 + (1/6)\gamma ···E^3+ ...\,\!</math> (2)
where:
- <math>\mu_0\,\!</math> is the permanent dipole of the molecule,
- <math>\alpha\,\!</math> is the polarizability of the molecule (the microscopic equivalent to <math>\chi^{(1)}\,\!</math>),
- <math>\beta\,\!</math> and <math>\gamma\,\!</math> are the first and second hyperpolarizabilities, respectively.
As for the susceptibilities, <math>\alpha\,\!</math>, <math>\beta\,\!</math>, and <math>\gamma\,\!</math> are tensors of progressively higher rank, are frequency dependent, and each component can be a complex quantity. <math>\beta\,\!</math> is zero for centrosymmetric molecules.
Under normal conditions,
- <math>\alpha_{ij} E_j > \beta_{ijk} E_j · E_k > \gamma_{ijkl} E_j · E_k · E_l \,\!</math>
(here we have introduced the subscript to identify a specific component of the tensors and vectors; i, j, k, l = x, y, z). However, for field strengths large enough or for specific frequencies of the electromagnetic field, one of the nonlinear terms may become the dominant contribution to the dipole moment. Typically, high intensity laser beams are need for the effects of the hyperpolarizabilities to become observable.
Third-order Nonlinear Polarization of Matter
It can be shown that the description of Eq. (2) above corresponds to the behavior of a molecule in an anharmonic potential well. Second-order NLO effects arise from a cubic component in the potential as a function of displacement from the equilibrium position. A quartic term in the potential is at the origin of third-order effects. This is illustrated in the graph at right. If the correction is added in a positive way the well becomes steeper, adding the correction in a negative way the potential well is more shallow. The change is symmetric with respect to x = 0. The curves shown are greatly exaggerated, in reality the deviation would be less than the thickness of the lines as they are drawn. For the most part during normal oscillations the electrons are held within a quadratic potential. Only when there is a large electric field is there a deviation of the electron from their resting position to the point where these terms (terms which account for anharmonicity) are manifested in any significant way. When a restoring force of x4 is added to a molecule the polarization deviates from that characteristic of the harmonic potential. A greater displacement means that it is getting harder to polarize the molecule the greater the difference between the harmonic potential and the quartic potential. A material with a greater susceptibility has a higher refractive index (and a higher dielectric constant). If, as you polarize this material more and more it becomes harder to polarize, its susceptibility decreases with the field, as does its refractive index.
Third-Order NLO Effects
Nonlinear Self-Focusing
Let's consider a beam of light propagating into a NLO material with a positive nonlinear refractive index. If the intensity distribution in the beam is higher in the center than at the edge, the material that is near the center of the beam, where the intensity is highest, will have a higher refractive index than the material at the edge of the beam profile, where there is low intensity. The refractive index changes because in this NLO material the polarizability (and susceptibility) depends in the intensity of the light, and thus the refractive index is also intensity dependent. As the refractive index is now different across the beam profile, the different portions of the beam will be refractive to different degrees, in particular the rays near the optical axis are refractive more than rays farther away from the axis. Thus this NLO material behaves like a lens that focuses light that propagates through it. In a focusing beam the cross-sectional area of the beam decreases as you approach the focal point and the intensity increases (because there are more photons in the unit area). So, as a beam becomes focused the added intensity increases the refractive index further, causing even more focussing, higher intensity at the center of the beam and more change in refractive index. This process is called “nonlinear self-focusing”.

All materials (including glass and air) have third order non-linear optical effects. Sometimes these effects can lead to catastrophic self-focusing, leading to the destruction of the material when the intensity becomes too high. Catastrophic self-focusing thus poses limits to the maximum intensities within optical materials, for example those used in lasers. Usually, a material with fewer defects is less likely to be damaged (or will damage at higher intensities). When doing experiments involving frequency tripling researchers need to use perfect defect-free crystals.
In an NLO material in which polarization decreases with the light intensity (a material with a negative nonlinear refractive index), the opposite effect is observed: the refractive index encountered by the beam while propagating in the medium is smaller at the center of the beam and larger near the edges, leading to self-defocusing of the beam. Thus, the beam passing through this material has a tendency to spread out.
Positive and negative γ and positive and negative χ(3) lead to different effects. Specifically, negative χ(3) leads to self-defocusing, and positive χ(3) leads to self-focusing.
See Wikipedia Self Focusing
See also Encyclopedia of Laser Physics Self Focusing
Third Harmonic Generation and the Optical Kerr Effect
If we reconsider equation (2) for the expansion of dipole moment of a molecule as a function of electric field, assuming that the even-order terms are zero (i.e., that the molecule is centrosymmetric), and we apply an oscillating field at frequency ω:
- <math>E = E_0 cos(\omega t) \,\!</math>
the dipole moment of the molecule becomes:
- <math>\mu = \alpha E_0 cos(\omega t) + (1/6) \gamma E_0^3cos^3 (\omega t) + ...\,\!</math> (3)
From trigonometry it can be shown that:
- <math>cos^3(\omega t) = (3/4) cos(\omega t) + (1/4) cos (3\omega t)\,\!</math> (4)
Substituting (4) in (3), we obtain:
- <math>\mu = \alpha E_0 cos(\omega t) + (1/6) \gamma E_0^3 (3/4) cos(\omega t) + (1/6) \gamma E_0^3 (1/4) cos (3\omega t)\,\!</math>
or, equivalently:
- <math>\mu= [\alpha +(1/6) \gamma E_{0}^{2}(3/4)]E_0cos(\omega t) + (1/6) \gamma E_0^3(1/4)cos(3\omega t)\,\!</math> (5)
Thus, the material has an effective polarizability that depends on E02 (the maximum deviation of the sinusoidal electric field) and γ. This is called Kerr effect. E02 is always positive. On the other hand γ can be either positive or negative. Thus, by increasing the magnitude of the electric field, the polarizability of the material increases if γ is positive and decreases if γ is negative. If E is the electric field of an electromagnetic wave, due to this third-order effect the linear polarizability can be changed simply by modifying the intensity of the applied light (because the light intensity is proportional to E02).
This component of the dipole moment or polarization oscillates at the same frequency of the input field, ω. We note that the :<math>[\alpha + (1/6) \gamma E_{0}^{2}(3/4)]\,\!</math> term of equation (5) is similar to the term leading to the linear electrooptic effect or the Pockels effect.
There are two kinds of Kerr effects. In an optical frequency Kerr effect a very high intensity beam is used to changed the refractive index of a material at the same frequency the beam.
The DC Kerr effect or the quadratic electro-optic effect involves a low intensity beam combined with an oscillating applied voltage that can modulate the refractive index.
It can be seen that equation (5) also contain a term at frequency 3ω, the third harmonic of the incident field:
- <math> (1/6) \gamma E_0^3(1/4)cos(3\omega t)\,\!</math>
The magnitude of this component depends on γ. Thus, the interaction of light with a third-order NLO material will create a polarization component at its third harmonic. Likewise, at the macroscopic level, in the presence of a strong laser beam at frequency ω the bulk material will have an induced polarization at 3ω, due to χ(3). This process is called third-harmonic generation.
Four Wave Mixing
Third harmonic generation is a four wave mixing process: three waves (electric fields 1, 2 and 3 at frequency ω) interact in a material to create a fourth wave (at frequency 3ω). In the case of third harmonic generation with a single beam of light the three fields are degenerate: electric field 1 has the same frequency, phase and momentum (k vector) as electric field 2 and 3.
This does not have to be the case. There could be three beams with different phases and different directions, or different polarizations. If the frequency components of the fields are different other nonlinear effects can be observed, for example, the fields can "mix" and produce new fields with frequency equal to the sums and differences of frequencies of the input fields (four wave mixing):
- <math>\omega_1 + \omega_2 + \omega_3\,\!</math> (this is third harmonic generation if ω1 = ω2 = ω3)
or
- <math>\omega_1 + \omega_2 - \omega_3\,\!</math>
If the frequencies are the same, the latter situation yields light out at the same frequency as the input and is called degenerate four wave mixing (in the case of a single beam, this leads to the self-focusing effect discussed earlier).
Another way to describe the degenerate four wave mixing (DFWM) process is to consider two beams of light (at the same frequency) interacting within a material to create an interference pattern and thus a spatially periodic variation in light intensity in the material. As we have noted before, the induced change in refractive index of a third-order nonlinear optical material is proportional to the intensity of the applied field. Thus, if two beams are interfering in a third-order NLO material, the result will be a refractive index grating, that is a periodic modulation of the refractive index in the areas of constructive and destructive interference: the areas that are brightest will have an increased refractive index (with a positive χ(3)); at the darkest point the refractive index will have zero change. When a third beam is incident on this grating, the beam is diffracted from the grating, generating a fourth beam, called the phase conjugate. This process is called four wave mixing: two writing beams and a probe beam result in a fourth phase-conjugate beam.
Phase Conjugation
A potential use of Degenerate Four-wave Mixing (DFWM) is in phase conjugate optics.
A beam of light has a momentum determined by the direction it is traveling. If beams of light mix and do not transfer energy to the material the momentum must be conserved. Two counter-propagating beams with the same phase have a momentum sum of zero. If the probe beam is counter-propagating with respect to one of the writing beams in a DFWM configuration, then the diffracted beam exactly retraces the path of the other writing beam. Phase conjugate optics takes advantage of this special feature of the diffracted beam. As a result, a pair of diverging beams impinging on a phase conjugate mirror will converge after "reflection". In contrast, a pair of diverging beams reflected from an ordinary mirror will continue to diverge.
One consequence of this is that distorted optical wavefronts can be reconstructed using phase conjugate optical systems, as described in the next subsection.
Phase Conjugate Mirror
The figure at right illustrates the operation of a phase conjugate mirror. A planar wave (a) passes through a distorting material (rectangle), which introduces an aberration in the wavefront. Then the light interacts with a phase conjugate mirror (gray area) creating the phase conjugate wavefront (c). Then the phase conjugate wave passes through the distorting material on the reverse path, canceling the original aberration thus producing an undistorted wavefront (d). Aberrations in the wavefront can be caused by the medium not having a uniform refractive index, so that portions of the light will travel faster than others, and leading to a deformation in the original wavefront. When the wavefront hits the phase conjugate mirror, the propagation direction of the beam reversed, but the shape of the wavefront is not changed: the part of the beam that comes into the mirror first ends up leaving last and viceversa. When the reversed beam travels back and encounters the original material, portions of the beam are going to be slowed, other sped up, as previously, but now the process acts on a distorted wavefront. The result is that distortion produced by the second pass exactly cancels that of the first pass, thus the aberration is removed and the original wavefront is obtained.
In the following Flash animation a wavefront of light passes through a material with uneven index of refraction. Select either "normal mirror" or "phase conjugate mirror" to see the effect on the final wavefront after passing through the medium twice.
<swf width="500" height="400">images/e/e7/Conjugatemirror.swf</swf>
There are applications for this when looking at distant objects that have passed through a material that is scattering. If you bounce the light off a phase conjugate mirror in two passes, you can get back the original undistorted image. This is useful for targeting applications and for looking at images of the Earth from a satellite where there are distortions due to inhomogeneities in the atmosphere. This is a third order nonlinear optical effect.
See wikipedia:Nonlinear_optics#Optical_phase_conjugation
Second Hyperpolarizability and BOA
The figure at right displays how the second hyperpolarizability γ varies as a function of bond-order alternation (BOA) in a one-dimensional polymethine structure. The tensor component included in the plot is xxxx, where x represents the long axis of the molecule (the other components are negligible for these systems). As introduced elsewhere, BOA is the average value of the difference between the length of adjacent CC bonds in the chain [[2]]. The left side of the plot corresponds to the polyene limit (large and negative BOA), the cyanine-like limit corresponds to BOA = 0, and the zwitterionic limit to large and positive BOA. γxxxx (red dots) is calculated using perturbation theory. It can be noted that γ starts positive in the polyene limit, goes through a maximum, then through zero before assuming a large negative value at the cyanine-like limit; the behavior is symmetrical on the BOA > 0 side of the plot .
If only few states contribute to the perturbation expression for γ, it is possible to write a simplified equation that contains three terms, dubbed n (negative), tp (two-photon) and d (dipolar, because it only comes into effect when there is a change in dipole moment between the ground and the excited state):
- <math>\gamma_{model} \propto - \left ( \frac {\mu^{4}_{ge}} {E^{3}_{ge}} \right) + \sum_{e^\prime} \left( \frac {\mu^{2}_{ge} \mu^{2}_{ee^\prime}} {E^{2}_{ge} E_{ge^\prime}} \right ) + \left ( \frac {\mu^{2}_{ge} (\mu_{ee} - \mu_{gg})^{2}} {E^{3}_{ge}} \right )\,\!</math>
where:
g is the ground state, e the lowest excited state. The summation in the middle term is over two-photon allowed states, e', in the system.
- <math>\mu_{ab}\,\!</math> is the transition dipole moment between the states a and b.
- <math> E_{ab}\,\!</math> is the energy difference between the states a and b.
In the n term (leftmost term in the equation), the transition dipole moment between the ground and the initial state comes in at the 4th power and is divided by the energy gap between those two states to the third power. This term is always negative and it assumes the largest absolute value at the cyanine limit.
The tp term (middle term in the equation) depends on the transition dipole moment between the ground and the excited state, and between the excited state and a higher lying two-photon state, both squared. This term is positive, with a maximum for BOA = 0.
The d term (rightmost term in the equation) is similar to that that appears in simplified expressions for the hyperpolarizability β. The difference in dipole moment is squared so that it always positive, the energy term is cubed. The two positive maxima in γ can be traced mostly to this term.
The value of each of these terms as a function of BOA and their sum, γmodel (open circles), are displayed in the plot. The values of γmodel are similar to those of γxxxx, indicating that the simplified model is sufficient to account for the main changes in the magnitude and sign of the hyperpolarizability for this class of compounds.
Third-order Nonlinear Optical Properties of Polarized Polyenes
Beta-carotene is an organic compound with a long polyenic chain, it is orange-red and it is found in many fruits and vegetables.
Derivatives of beta-carotene have been synthesized with acceptor groups of various strengths on one end of the chain, to test the effect on the polarizability and hyperpolarizability of the molecule. This table reports the values of γ for a series of these derivatives. It can be seen that the magnitude of γ increases by a factor of 45 when the strength of the acceptor is increased. This is also accompanied by a red-shift in the position of the absorption maximum. The increase in γ can be explained by a change in the BOA value in the presence of acceptor groups, as BOA becomes less negative going from the initial polyene (symmetric structure, no acceptor; see top row) to a molecule with strong acceptor on one side (bottom row). As seen in the plot in the previous subsection, this type of change in BOA is accompanied by an increase in γ.
Summary
Third-order nonlinear effects can be described in terms of the molecular parameter hyperpolarizability γ or the bulk susceptibility χ(3). These quantities depend on the frequency of the electromagnetic waves interacting in a material and different effects can be observed as a function of these frequencies. These are also complex quantities. In the case of the linear polarizability, the real part is related to how light is refracted by the material, the imaginary part is related to the absorption of light by the material. The situation is similar for γ. Molecules will have both real and imaginary parts to γ. The real part affects to how the refractive index is changed as light of a given intensity goes through it (the refractive index is field-dependent in these materials). The imaginary part is manifested in two-photon absorption. An intensity dependent refractive index can lead to self-focussing or self-defocussing of a beam propagating through a layer of material. Other third-order optical effects that can be exploited for applications are sum (or difference) frequency generation and wave mixing.
In order to make useful devices like the Mach Zehnder interferometer you want to use a material whose index of refraction can be changed using a light beam, but you don’t want to lose light in the material because of linear absorption or scattering. They can also lose transparency at a high intensity due to the process of two-photon absorption. The identification of materials with large γs at the desired wavelength and low loss is an active area of research. Dipolar molecules tend to have large positive γ values but also tend to have high two-photon absorption cross sections. Recently it has been reported that a class of molecules with negative γ have very large real parts of the hyperpolarizability but, in certain spectral regions , their imaginary part is almost zero so there would be no light lost due to two-photon absorption. These are good candidates for all optical switching applications because until now molecules with high γ (χ(3)) have had a high a loss due to two-photon absorption.
see also All Optical Switching
| Return to Third-order Processes, Materials & Characterization Menu | Next Topic |